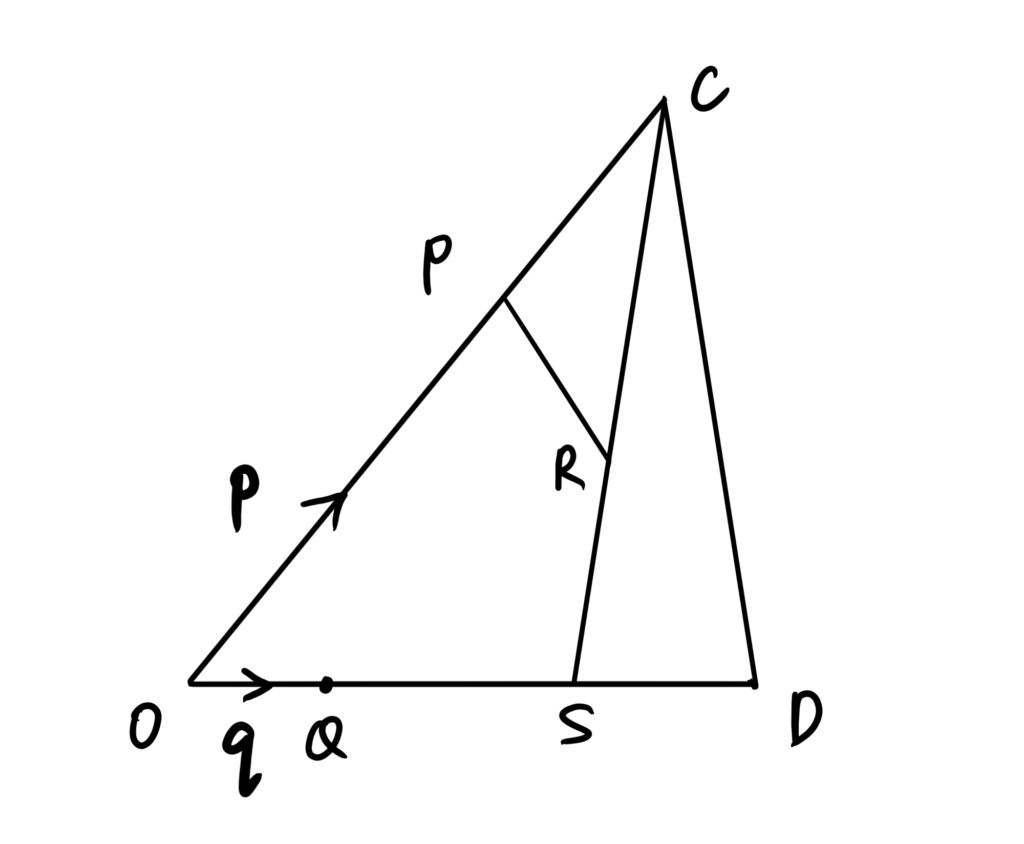
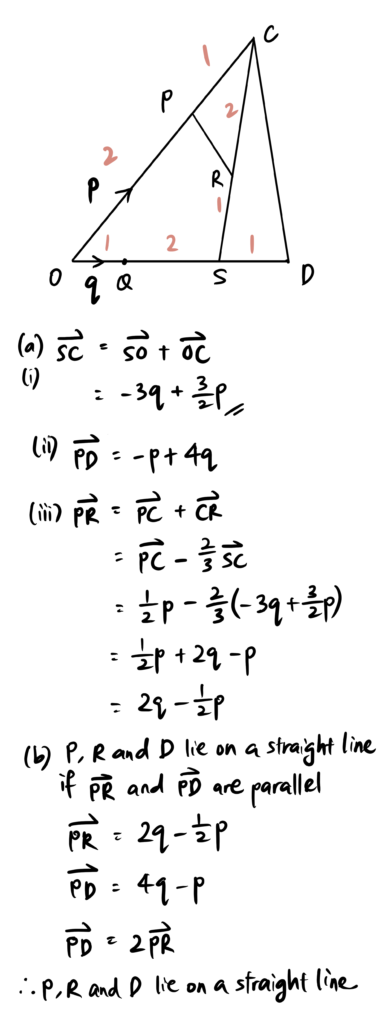7.8. Determine if points are collinear and calculate ratio of areas 2
G7. Vectors in two dimensions

Question

In the diagram below, $\vec{OP}$ = p and $\vec{OQ}$ = q. It is given that $\vec{OP}$ = $\frac{2}{3}\vec{OC}$ , $\vec{OQ}$ = $\frac{1}{3}\vec{OS}$ , OQ = SD and SC = 3SR.

(a) Express, as simply as possible, in terms of p and q.
(i) $\vec{SC}$ [1]
(ii) $\vec{PD}$ [1]
(iii) $\vec{PR}$ [2]

(b) Prove that P, R and D lie on a straight line. [2]

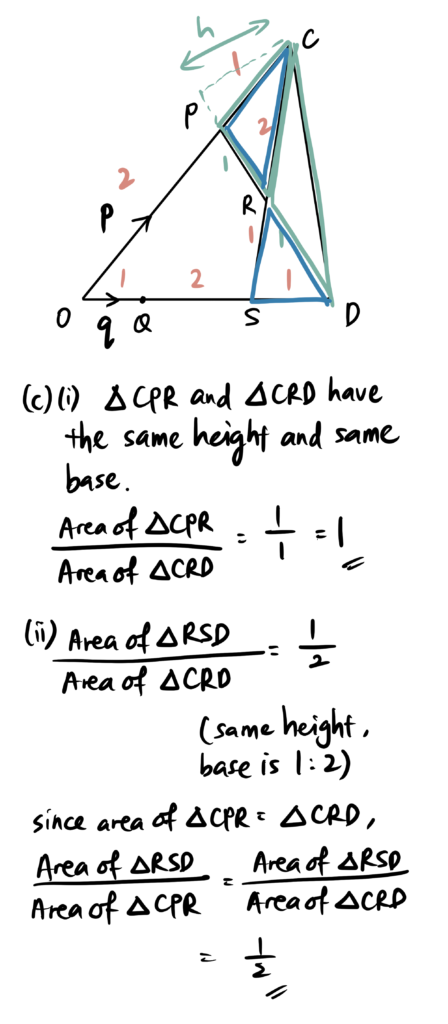
(c) Find the numerical value of
(i) $\frac{Area of \triangle{CPR}}{Area of \triangle{CRD}}$ [1]
(ii) $\frac{Area of \triangle{RSD}}{Area of \triangle{CPR}}$ [2]